Weierstrass (weird) function

In mathematics, the Weierstrass function is a pathological example of a real-valued function on the real line. The function has the property that it is continuous everywhere but differentiable nowhere. It is named after its discoverer Karl Weierstrass.

Historically, the Weierstrass function is important because it was the first published (1872) to challenge the notion that every continuous function was differentiable except on a set of isolated points.

Construction

In Weierstrass' original paper, the function was defined by

where 0 < a < 1, b is a positive odd integer, and

This construction, along with the proof that it is nowhere differentiable, was first given by Weierstrass in a paper presented to the Königliche Akademie der Wissenschaften on 18 July 1872.

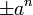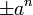The proof that this function is continuous everywhere is not difficult. Since the terms of the infinite series which defines it are bounded by and this has finite sum for 0 < a < 1, convergence of the sum of the terms is uniform by the Weierstrass M-test with M_n = aⁿ. Since each partial sum is continuous and the uniform limit of continuous functions is continuous, f is continuous.

To prove that it is nowhere differentiable, we consider an arbitrary point  and show that the function is not differentiable at that point. To do this, we construct two sequences of points x_n and x'_n which both converge to x, having the property that

Naively it might be expected that a continuous function must have a derivative, or that the set of points where it is not differentiable should be "small" in some sense. According to Weierstrass in his paper, earlier mathematicians including Gauss had often assumed that this was true. This might be because it is difficult to draw or visualise a continuous function whose set of nondifferentiable points is something other than a finite set of points. Analogous results for better behaved classes of continuous functions do exist, for example the Lipschitz functions, whose set of non-differentiability points must be a Lebesgue null set (Rademacher's theorem). When we try to draw a general continuous function, we usually draw the graph of a function which is Lipschitz and has other nice properties.

The Weierstrass function could perhaps be described as one of the very first fractals studied, although this term was not used until much later. The function has detail at every level, so zooming in on a piece of the curve does not show it getting progressively closer and closer to a straight line. Rather between any two points no matter how close, the function will not be monotone. The Hausdorff dimension of the classical Weierstrass function is bounded above by , (where a and b are the constants in the construction above) and is generally believed to be exactly that value, but this had not been proven rigorously.

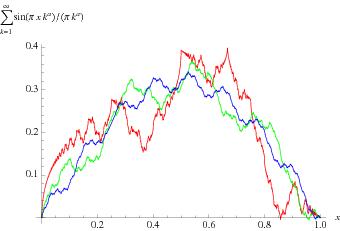
The term Weierstrass function is often used in real analysis to refer to any function with similar properties and construction to Weierstrass' original example. For example, the cosine function can be replaced in the infinite series by a piecewise linear "zigzag" function. G. H. Hardy showed that the function of the above construction is nowhere differentiable with the assumptions .

Hölder continuity

It is convenient to write the Weierstrass function equivalently as

for some 0 < α < 1. Then W_α(x) is Hölder continuous of exponent α, which is to say that there is a constant C such that

for all x and y. Moreover, W₁ Hölder continuous of all orders α < 1 but not Lipschitz continuous.

Density of nowhere differentiable functions

It turns out that the Weierstrass function is far from being an isolated example: although it is "pathological", it is also "typical" of continuous functions:

• In a topological sense: the set of nowhere-differentiable real-valued functions on [0, 1] is comeager in the vector space C([0, 1]; R) of all continuous real-valued functions on [0, 1] with the topology of uniform convergence.
• In a measure-theoretic sense: when the space C([0, 1]; R) is equipped with classical Wiener measure γ, the collection of functions that are differentiable at even a single point of [0, 1] has γ-measure zero. The same is true even if one takes finite-dimensional "slices" of C([0, 1]; R): the nowhere-differentiable functions form a prevalent subset of C([0, 1]; R).