Proof without words (Sum of odd numbers)

In mathematics, a proof without words is a proof of an identity or mathematical statement which can be demonstrated as self-evident by a diagram without any accompanying explanatory text. Such proofs can be considered more elegant than more formal and mathematically rigorous proofs due to their self-evident nature. When the diagram demonstrates a particular case of a general statement, to be a proof, it must be able to be generalised.

Sum of odd numbers

The statement that the sum of all positive odd numbers up to 2n − 1 is a perfect square—more specifically, the perfect square n²—can be demonstrated by a proof without words, as shown below. The first square is formed by 1 block; 1 is the first square. The next strip, made of white squares, shows how adding 3 more blocks makes another square: four. The next strip, made of black squares, shows how adding 5 more blocks makes the next square. This process can continue indefinitely.

Unexpected hanging paradox

The unexpected hanging paradox, hangman paradox, unexpected exam paradox, surprise test paradox or prediction paradox is a paradox about a person's expectations about the timing of a future event (e.g. a prisoner's hanging, or a school test) which he is told will occur at an unexpected time.

Despite significant academic interest, there is no consensus on its precise nature and consequently a final 'correct' resolution has not yet been established. One approach, offered by the logical school of thought, suggests that the problem arises in a self-contradictory self-referencing statement at the heart of the judge's sentence. Another approach, offered by the epistemological school of thought, suggests the unexpected hanging paradox is an example of an epistemic paradox because it turns on our concept of knowledge. Even though it is apparently simple, the paradox's underlying complexities have even led to it being called a "significant problem" for philosophy.

New prime number: The biggest ever found

The record for biggest prime number ever discovered has been shattered again. The latest holder of the title has 17,425,170 digits — over four million more than the previous "biggest" prime number, discovered in 2008, says a news release from the Great Internet Mersenne Prime Search (GIMPS), the distributed computing project that found it.

This is the beginning of the new record-setting prime number, which continues for more than 17 million more digits. (GIMPS)

Fermat's little theorem

Fermat's little theorem states that if p is a prime number, then for any integer a, the number a ^p − a is an integer multiple of p. In the notation of modular arithmetic, this is expressed as

For example, if a = 2 and p = 7, 2⁷ = 128, and 128 − 2 = 7 × 18 is an integer multiple of 7.

If a is not divisible by p, Fermat's little theorem is equivalent to the statement that a ^p − 1 − 1 is an integer multiple of p:

For example, if a = 2 and p = 7, 2⁶ = 64, and 64 − 1 = 63 = 7 × 9.

Fermat's little theorem is the basis for the Fermat primality test and is one of the fundamental results of elementary number theory. The theorem is named after Pierre de Fermat, who stated it in 1640. It is called the "little theorem" to distinguish it from Fermat's last theorem.

Mathematics of planet earth 2013

Dozens of scientific societies, universities, research institutes, and foundations all over the world have banded together to dedicate 2013 as a special year for the Mathematics of Planet Earth.

Our planet is the setting for dynamic processes of all sorts, including the geophysical processes in the mantle, the continents, and the oceans, the atmospheric processes that determine our weather and climates, the biological processes involving living species and their interactions, and the human processes of finance, agriculture, water, transportation, and energy. The challenges facing our planet and our civilization are multidisciplinary and multifaceted, and the mathematical sciences play a central role in the scientific effort to understand and to deal with these challenges.

The Birthday Problem

In probability theory, the birthday problem or birthday paradox concerns the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 367 (since there are 366 possible birthdays, including February 29). However, 99% probability is reached with just 57 people, and 50% probability with 23 people. These conclusions are based on the assumption that each day of the year (except February 29) is equally probable for a birthday.

The mathematics behind this problem led to a well-known cryptographic attack called the birthday attack, which uses this probabilistic model to reduce the complexity of cracking a hash function.

√2 is irrational

Theorem: The square root of 2 is irrational, 

Proof

Assume for the sake of contradiction that . Hence 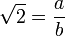 holds for some a and b that are coprime.

This implies that . Rewriting this gives .

Since the left-hand side of the equation is divisible by 2, then so must the right-hand side, i.e., . Since 2 is prime, we must have that .

So we may substitute a with , and we have that .

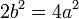Dividing both sides with 2 yields , and using similar arguments as above, we conclude that . However, we assumed that  such that that a and b were coprime, and have now found that  and ; a contradiction.

Therefore, the assumption was false, and  cannot be written as a rational number. Hence, it is irrational.

Gauss-Markov Theorem

Simplex Method Examples

Law of total variance

In probability theory, the law of total variance or variance decomposition formula, also known by the acronym EVVE (or Eve's law for short), states that if X and Y are random variables on the same probability space, and the variance of Y is finite, then

In language perhaps better known to statisticians than to probabilists, the two terms are the "unexplained" and the "explained component of the variance"

The nomenclature in this article's title parallels the phrase law of total probability. Some writers on probability call this the "conditional variance formula" or use other names.

Note that the conditional expected value E( Y | X ) is a random variable in its own right, whose value depends on the value of X. Notice that the conditional expected value of Y given the event X = y is a function of y (this is where adherence to the conventional rigidly case-sensitive notation of probability theory becomes important!). If we write E( Y | X = y ) = g(y) then the random variable E( Y | X ) is just g(X). Similar comments apply to the conditional variance.

Apparent Paradox

1.  Exactly one of these statements is false.
2. Exactly two of these statements are false.
3. Exactly three of these statements are false.
4. Exactly four of these statements are false.
5. Exactly five of these statements are false.
6. Exactly six of these statements are false.
7. Exactly seven of these statements are false.
8. Exactly eight of these statements are false.
9. Exactly nine of these statements are false
10. Exactly ten of these statements are false. 

How many of them are true?If any , which ones?

Mathematics and Reality

The question is sometimes raised as to how it is that mathematics, which is a creation of the human mind, without any empirical reference to external reality, should match reality so well. When we make the distinction between the reality we experience and the underlying reality, the correlation between mathematics and reality is not so surprising.

Science takes our observations of the external world and seeks to understand how they occur and to discover underlying patterns and principles. In doing so, it inevitably draws upon experience When atoms were first imagined, they were thought of as small solid balls of matterÑa model clearly drawn from everyday experience. Then, as physics realized that atoms were composed of more elementary particles (even the word "particle" contains an implicit assumption as to their nature), the model shifted to one of a central nucleus surrounded by orbiting electronsÑagain based on experience at the human level. Now, as we try to interpret quantum theory, we inevitably draw upon other concepts derived from our perception of reality. We interpret them as waves or bundles of energy, possessing "spin" and mass. Yet every model we come up with, fails in some way or another to capture the essence of the underlying reality.

Kepler–Poinsot polyhedra

In geometry, a Kepler–Poinsot polyhedron is any of four regular star polyhedra. They may be obtained by stellating the regular convex dodecahedron and icosahedron, and differ from these in having regular pentagrammic faces or vertex figures.

The four Kepler–Poinsot polyhedra are illustrated above. Each is identified by its Schläfli symbol, of the form {p, q}, and by its name. One face of each figure is shown yellow and outlined in red.

Descartes' rule of signs

In mathematics, Descartes' rule of signs, first described by René Descartes in his work La Géométrie, is a technique for determining the number of positive or negative real roots of a polynomial.

The rule gives us an upper bound number of positive or negative roots of a polynomial. It is not a complete criterion, i.e. it does not tell the exact number of positive or negative roots.

Polarization identity

In mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let  denote the norm of vector x and  the inner product of vectors x and y. Then the underlying theorem, attributed to Fréchet, von Neumann and Jordan, is stated as:

In a normed space (V, ), if the parallelogram law holds, then there is an inner product on V such that  for all .