The Gaussian integral, also known as the Euler–Poisson integral is the integral of the Gaussian function e−x2 over the entire real line. It is named after the German mathematician and physicist Carl Friedrich Gauss. The integral is:
This integral has wide applications. For example, with a slight change of variables it is used to compute the normalizing constant of the normal distribution. The same integral with finite limits is closely related both to the error function and the cumulative distribution function of the normal distribution.
Although no elementary function exists for the error function, as can be proven by the Risch algorithm, the Gaussian integral can be solved analytically through the tools of calculus. That is, there is no elementary indefinite integral for  , but the definite integral
, but the definite integral  can be evaluated.
can be evaluated.
 , but the definite integral
, but the definite integral  can be evaluated.
can be evaluated.
The Gaussian integral is encountered very often in physics and numerous generalizations of the integral are encountered in quantum field theory.
Brief proof
Briefly, using the method above, one computes that on the one hand,
On the other hand,
where the factor of r comes from the transform to polar coordinates (r dr dθ is the standard measure on the plane, expressed in polar coordinates), and the substitution involves taking s = −r2, so ds = −2r dr.
Combining these yields
so
 .
.
Careful proof
To justify the improper double integrals and equating the two expressions, we begin with an approximating function:

If the integral  were absolutely convergent we would have that its Cauchy principal value, that is, the limit
were absolutely convergent we would have that its Cauchy principal value, that is, the limit
 were absolutely convergent we would have that its Cauchy principal value, that is, the limit
were absolutely convergent we would have that its Cauchy principal value, that is, the limit
would coincide with  . To see that this is, in fact, the case consider
. To see that this is, in fact, the case consider
 . To see that this is, in fact, the case consider
. To see that this is, in fact, the case consider
so we can compute  by just taking the limit
by just taking the limit  .
.
 by just taking the limit
by just taking the limit  .
.
Taking the square of I(a) yields
Using Fubini's theorem, the above double integral can be seen as an area integral
taken over a square with vertices {(−a, a), (a, a), (a, −a), (−a, −a)} on the xy-plane.
Since the exponential function is greater than 0 for all real numbers, it then follows that the integral taken over the square's incircle must be less than  , and similarly the integral taken over the square's circumcircle must be greater than
, and similarly the integral taken over the square's circumcircle must be greater than  . The integrals over the two disks can easily be computed by switching from cartesian coordinates to polar coordinates:
. The integrals over the two disks can easily be computed by switching from cartesian coordinates to polar coordinates:
 , and similarly the integral taken over the square's circumcircle must be greater than
, and similarly the integral taken over the square's circumcircle must be greater than  . The integrals over the two disks can easily be computed by switching from cartesian coordinates to polar coordinates:
. The integrals over the two disks can easily be computed by switching from cartesian coordinates to polar coordinates:
(See to polar coordinates from Cartesian coordinates for help with polar transformation.)
Integrating,
By the squeeze theorem, this gives the Gaussian integral
By Cartesian coordinates
A different technique, which goes back to Laplace (1812), is the following.
Let
Since the limits on  as
as  goes to
goes to  depend on the sign of
depend on the sign of  , it simplifies the calculation to use the fact that
, it simplifies the calculation to use the fact that 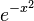 is an even function, and, therefore, the integral over all real numbers is just twice the integral from zero to infinity. That is,
is an even function, and, therefore, the integral over all real numbers is just twice the integral from zero to infinity. That is,  . Thus, over the range of integration,
. Thus, over the range of integration,  , and the variables
, and the variables  and
and  have the same limits. This yields:
have the same limits. This yields:
 as
as  goes to
goes to  depend on the sign of
depend on the sign of  , it simplifies the calculation to use the fact that
, it simplifies the calculation to use the fact that 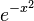 is an even function, and, therefore, the integral over all real numbers is just twice the integral from zero to infinity. That is,
is an even function, and, therefore, the integral over all real numbers is just twice the integral from zero to infinity. That is,  . Thus, over the range of integration,
. Thus, over the range of integration,  , and the variables
, and the variables  and
and  have the same limits. This yields:
have the same limits. This yields:
Then
Finally,  , as expected.
, as expected.
 , as expected.
, as expected.Relation to the Gamma function
The integrand is an even function,
Thus, after the change of variable  , this turns into the Euler integral
, this turns into the Euler integral
 , this turns into the Euler integral
, this turns into the Euler integral
where Γ is the gamma function. This shows why the factorial of a half-integer is a rational multiple of  . More generally,
. More generally,
 . More generally,
. More generally,










![\begin{align}
\frac{I^2}{4} & = \int_0^\infty \left( \int_0^\infty e^{-(x^2 + y^2)} \, dy \right) \, dx = \int_0^\infty \left( \int_0^\infty e^{-x^2(1+s^2)} x\,ds \right) dx \\[5pt]
& = \int_0^\infty \left( \int_0^\infty e^{-x^2(1 + s^2)} x \, dx \right) \, ds \\[5pt]
& = \int_0^\infty \left[ \frac{1}{-2(1+s^2)} e^{-x^2(1+s^2)} \right]_0^\infty \, ds
= \frac{1}{2} \int_0^\infty \frac{ds}{1+s^2} \\[5pt]
& = \frac{1}{2} \left. \arctan s \frac{}{} \right|_0^\infty = \frac{\pi}{4}.
\end{align}](http://upload.wikimedia.org/wikipedia/en/math/3/8/0/3807a364a4ceec7ea40a3d7c57b6beaa.png)


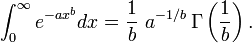
No comments:
Post a Comment