In mathematics, the polarization identity is any one of a family of formulas that express the inner product of two vectors in terms of the norm of a normed vector space. Let  denote the norm of vector x and
denote the norm of vector x and  the inner product of vectors x and y. Then the underlying theorem, attributed to Fréchet, von Neumann and Jordan, is stated as:
the inner product of vectors x and y. Then the underlying theorem, attributed to Fréchet, von Neumann and Jordan, is stated as:
In a normed space (V,  denote the norm of vector x and
denote the norm of vector x and  the inner product of vectors x and y. Then the underlying theorem, attributed to Fréchet, von Neumann and Jordan, is stated as:
the inner product of vectors x and y. Then the underlying theorem, attributed to Fréchet, von Neumann and Jordan, is stated as: ), if the parallelogram law holds, then there is an inner product on V such that
), if the parallelogram law holds, then there is an inner product on V such that  for all
for all  .
.Formula
The various forms given below are all related by the parallelogram law:
The polarization identity can be generalized to various other contexts in abstract algebra, linear algebra, and functional analysis.
For vector spaces with real scalars
If V is a real vector space, then the inner product is defined by the polarization identity
For vector spaces with complex scalars
If V is a complex vector space the inner product is given by the polarization identity:
where i = √(−1) . Note that this defines an inner product which is linear in its first and semilinear in its second argument. To adjust for contrary definition, one needs to take the complex conjugate.
Multiple special cases for the Euclidean norm
A special case is an inner product given by the dot product, the so-called standard or Euclidean inner product. In this case, common forms of the identity include:
Relation to the law of cosines
The second form of the polarization identity can be written as
This is essentially a vector form of the law of cosines for the triangle formed by the vectors u, v, and u – v. In particular,
where θ is the angle between the vectors u and v.
Derivation
The basic relation between the norm and the dot product is given by the equation
Then
and similarly
Forms (1) and (2) of the polarization identity now follow by solving these equations for u · v, while form (3) follows from subtracting these two equations. (Adding these two equations together gives the parallelogram law.)




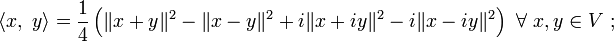
![\begin{array}{lr}
\textbf{u}\cdot\textbf{v} = \displaystyle\frac{1}{2}\left(\|\textbf{u}+\textbf{v}\|^2 - \|\textbf{u}\|^2 - \|\textbf{v}\|^2\right),\quad & (1) \\[1.5em]
\textbf{u}\cdot\textbf{v} = \displaystyle\frac{1}{2}\left(\|\textbf{u}\|^2 + \|\textbf{v}\|^2 - \|\textbf{u}-\textbf{v}\|^2 \right), & (2) \\[1.5em]
\textbf{u}\cdot\textbf{v} = \displaystyle\frac{1}{4}\left(\|\textbf{u}+\textbf{v}\|^2 - \|\textbf{u}-\textbf{v}\|^2 \right). & (3)
\end{array}](http://upload.wikimedia.org/math/a/f/9/af978de589a5f3c294540faf139d48be.png)



![\begin{alignat}{2}
\|\textbf{u}+\textbf{v}\|^2 &= (\textbf{u}+\textbf{v})\cdot(\textbf{u}+\textbf{v}) \\[3pt]
&= (\textbf{u}\cdot\textbf{u}) + (\textbf{u}\cdot\textbf{v}) + (\textbf{v}\cdot\textbf{u}) + (\textbf{v}\cdot\textbf{v}) \\[3pt]
&= \|\textbf{u}\|^2 + \|\textbf{v}\|^2 + 2(\textbf{u}\cdot\textbf{v}),
\end{alignat}](http://upload.wikimedia.org/math/c/f/e/cfeb63347580ef3dec94f76c5f4b86ce.png)
No comments:
Post a Comment