Malfatti Circles

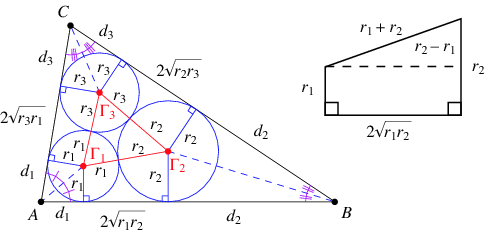
In geometry, the Malfatti circles are three circles inside a given triangle such that each circle is tangent to the other two and to two sides of the triangle. They are named after Gian Francesco Malfatti, who made early studies of the problem of constructing these circles in the mistaken belief that they would have the largest possible total area of any three disjoint circles within the triangle. Malfatti's problem has been used to refer both to the problem of constructing the Malfatti circles and to the problem of finding three area-maximizing circles within a triangle.

Malfatti's Problem

In 1803 Gian Francesco Malfatti posed the problem of cutting three cylindrical columns out of a rectangular wedge of marble, maximizing the total volume of the columns. He assumed, as did many others after him, that the solution to this problem was given by three tangent circles within the triangular cross-section of the wedge. That is, more abstractly, he conjectured that the three Malfatti circles have the maximum total area of any three disjoint circles within a given triangle.

Malfatti published in Italian and his work may not have been read by many in the original. It was popularised for a wider readership in French by Joseph Diaz Gergonne in the first volume of his ``Annales" (1810/11), with further discussion in the second and tenth. However, this advertisement most likely acted as a filter, as Gergonne only stated the circle-tangency problem, not the area-maximizing one.

The conjecture is wrong; Lob and Richmond (1930), who went back to the original Italian text, observed that for some triangles a larger area can be achieved by a greedy algorithm that inscribes a single circle of maximal radius within the triangle, inscribes a second circle within the largest of the three remaining corners of the triangle, and inscribes a third circle within the largest of the five remaining pieces. The difference in area for an equilateral triangle is small, just over 1%, but as Howard Eves pointed out in 1946, for an isosceles triangle with a very sharp apex, the optimal circles (stacked one atop each other above the base of the triangle) have nearly twice the area of the Malfatti circles.

Goldberg (1967) showed that, for every triangle, the Lob–Richmond procedure produces three circles with larger area than the Malfatti circles, so the Malfatti circles are never optimal. Zalgaller and Los' (1994) classified all of the different ways that a set of maximal circles can be packed within a triangle; using their classification, they proved that the greedy algorithm always finds three area-maximizing circles, and they provided a formula for determining which packing is optimal for a given triangle. In his 1997 Ph.D. thesis, Melissen conjectured more generally that, for any integer n, the greedy algorithm finds the area-maximizing set of n circles within a given triangle; the conjecture is known to be true for n ≤ 3.