Greedy Algorithm

A greedy algorithm is an algorithm that follows the problem solving heuristic of making the locally optimal choice at each stage with the hope of finding a global optimum. On some problems, a greedy strategy need not produce an optimal solution, but nonetheless a greedy heuristic may yield locally optimal solutions that approximate a global optimal solution.

For example, a greedy strategy for the traveling salesman problem (which is of a high computational complexity) is the following heuristic: "At each stage visit an unvisited city nearest to the current city". This heuristic need not find a best solution but terminates in a reasonable number of steps; finding an optimal solution typically requires unreasonably many steps. In mathematical optimization, greedy algorithms solve combinatorial problems having the properties of matroids.

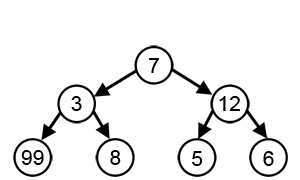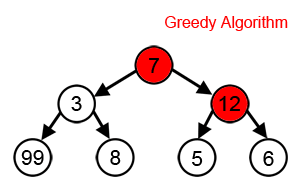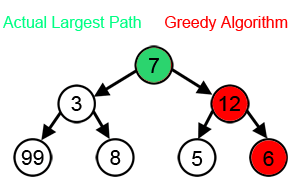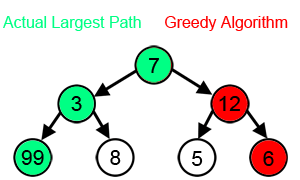
With a goal of reaching the largest-sum, at each step, the greedy algorithm will choose what appears to be the optimal immediate choice, so it will choose 12 instead of 3 at the second step, and will not reach the best solution, which contains 99.

Specifics

In general, greedy algorithms have five pillars:

1. A candidate set, from which a solution is created
2. A selection function, which chooses the best candidate to be added to the solution
3. A feasibility function, that is used to determine if a candidate can be used to contribute to a solution
4. An objective function, which assigns a value to a solution, or a partial solution, and
5. A solution function, which will indicate when we have discovered a complete solution

Greedy algorithms produce good solutions on some mathematical problems, but not on others. Most problems for which they work, will have two properties:

Greedy choice property 

We can make whatever choice seems best at the moment and then solve the subproblems that arise later. The choice made by a greedy algorithm may depend on choices made so far but not on future choices or all the solutions to the subproblem. It iteratively makes one greedy choice after another, reducing each given problem into a smaller one. In other words, a greedy algorithm never reconsiders its choices. This is the main difference from dynamic programming, which is exhaustive and is guaranteed to find the solution. After every stage, dynamic programming makes decisions based on all the decisions made in the previous stage, and may reconsider the previous stage's algorithmic path to solution.

Optimal substructure 

"A problem exhibits optimal substructure if an optimal solution to the problem contains optimal solutions to the sub-problems."

Cases of failure

For many other problems, greedy algorithms fail to produce the optimal solution, and may even produce the unique worst possible solution. One example is the traveling salesman problem mentioned above: for each number of cities there is an assignment of distances between the cities for which the nearest neighbor heuristic produces the unique worst possible tour.

Imagine the coin example with only 25-cent, 10-cent, and 4-cent coins. The greedy algorithm would not be able to make change for 41 cents, since after committing to use one 25-cent coin and one 10-cent coin it would be impossible to use 4-cent coins for the balance of 6 cent. Whereas a person or a more sophisticated algorithm could make change for 41 cents change with one 25-cent coin and four 4-cent coins.

Types

Greedy algorithms can be characterized as being 'short sighted', and as 'non-recoverable'. They are ideal only for problems which have 'optimal substructure'. Despite this, greedy algorithms are best suited for simple problems (e.g. giving change). It is important, however, to note that the greedy algorithm can be used as a selection algorithm to prioritize options within a search, or branch and bound algorithm. There are a few variations to the greedy algorithm:

• Pure greedy algorithms
• Orthogonal greedy algorithms
• Relaxed greedy algorithms