In probability theory, the law of total variance, Eve's Law, or variance decomposition formula states that if X and Y are random variables on the same probability space, and the variance of Y is finite, then
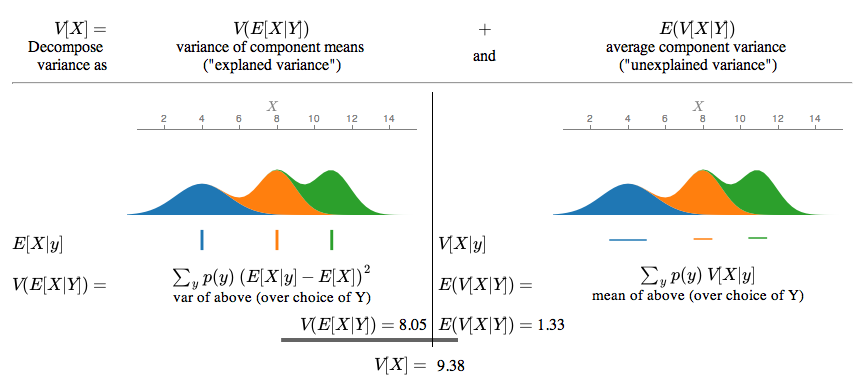
In language perhaps better known to statisticians than to probabilists, the two terms are the "unexplained" and the "explained component of the variance" (cf. fraction of variance unexplained, explained variation).
The nomenclature in this article's title parallels the phrase law of total probability. Some writers on probability call this the "conditional variance formula" or use other names.
Note that the conditional expected value E( Y | X ) is a random variable in its own right, whose value depends on the value of X. Notice that the conditional expected value of Y given theevent X = y is a function of y (this is where adherence to the conventional rigidly case-sensitive notation of probability theory becomes important!). If we write E( Y | X = y ) = g(y) then the random variable E( Y | X ) is just g(X). Similar comments apply to the conditional variance.
Proof
The law of total variance can be proved using the law of total expectation: First,
from the definition of variance. Then we apply the law of total expectation by conditioning on the random variable X:
Now we rewrite the conditional second moment of Y in terms of its variance and first moment:
Since expectation of a sum is the sum of expectations, we can now regroup the terms:
Finally, we recognize the terms in parentheses as the variance of the conditional expectation E[Y|X]:
-
![= \operatorname{E}\left[\operatorname{Var}[Y|X]\right] + \operatorname{Var}\left[\operatorname{E}[Y|X]\right]](http://upload.wikimedia.org/wikipedia/en/math/6/5/5/6559f15a7d296d42b7016554db0ca847.png)
- The square of the correlation
In cases where (Y, X) are such that the conditional expected value is linear; i.e., in cases where
it follows from the bilinearity of Cov(-,-) that
and
and the explained component of the variance divided by the total variance is just the square of the correlation between Y and X; i.e., in such cases,
One example of this situation is when (Y, X) have a bivariate normal (Gaussian) distribution.

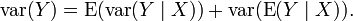
![\operatorname{Var}[Y] = \operatorname{E}[Y^2] - \operatorname{E}[Y]^2](http://upload.wikimedia.org/wikipedia/en/math/7/b/d/7bd46c99467c34f368931dd3c116640b.png)
![= \operatorname{E}\left[\operatorname{E}[Y^2|X]\right] - \operatorname{E}\left[\operatorname{E}[Y|X]\right]^2](http://upload.wikimedia.org/wikipedia/en/math/1/8/c/18c9e592f30fb729a0aad8b059f6d864.png)
![= \operatorname{E}\!\left[\operatorname{Var}[Y|X] + \operatorname{E}[Y|X]^2\right] - \operatorname{E}[\operatorname{E}[Y|X]]^2](http://upload.wikimedia.org/wikipedia/en/math/5/c/0/5c0704d067f5de2f4b120908b017cf54.png)
![= \operatorname{E}[\operatorname{Var}[Y|X]] + \left(\operatorname{E}\left[\operatorname{E}[Y|X]^2] - \operatorname{E}[\operatorname{E}[Y|X]\right]^2\right)](http://upload.wikimedia.org/wikipedia/en/math/c/d/b/cdb5e9e51cfd8ac6fb33a18541685e82.png)

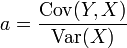


Excellent. Very well explained. Thank you.
ReplyDeleteHi, for some reason the LATEX in the second line of the proof does not properly render in the browser. Maybe missing something? $$?
ReplyDelete