The Basel problem is a famous problem in mathematical analysis with relevance to number theory, first posed by Pietro Mengoli in 1644 and solved by Leonhard Euler in 1735. Since the problem had withstood the attacks of the leading mathematicians of the day, Euler's solution brought him immediate fame when he was twenty-eight. Euler generalised the problem considerably, and his ideas were taken up years later by Bernhard Riemann in his seminal 1859 paper On the Number of Primes Less Than a Given Magnitude, in which he defined his zeta function and proved its basic properties. The problem is named after Basel, hometown of Euler as well as of the Bernoulli family who unsuccessfully attacked the problem.
The Basel problem asks for the precise summation of the reciprocals of the squares of the natural numbers, i.e. the precise sum of the infinite series:
The series is approximately equal to 1.644934 . The Basel problem asks for the exact sum of this series (in closed form), as well as a proof that this sum is correct. Euler found the exact sum to be  and announced this discovery in 1735. His arguments were based on manipulations that were not justified at the time, and it was not until 1741 that he was able to produce a truly rigorous proof.
and announced this discovery in 1735. His arguments were based on manipulations that were not justified at the time, and it was not until 1741 that he was able to produce a truly rigorous proof.
 and announced this discovery in 1735. His arguments were based on manipulations that were not justified at the time, and it was not until 1741 that he was able to produce a truly rigorous proof.
and announced this discovery in 1735. His arguments were based on manipulations that were not justified at the time, and it was not until 1741 that he was able to produce a truly rigorous proof.
Euler attacks the problem
Euler's original "derivation" of the value  is clever and original. He essentially extended observations about finite polynomials and assumed that these same properties hold true for infinite series. Of course, Euler's original reasoning requires justification, but even without justification, by simply obtaining the correct value, he was able to verify it numerically against partial sums of the series. The agreement he observed gave him sufficient confidence to announce his result to the mathematical community.
is clever and original. He essentially extended observations about finite polynomials and assumed that these same properties hold true for infinite series. Of course, Euler's original reasoning requires justification, but even without justification, by simply obtaining the correct value, he was able to verify it numerically against partial sums of the series. The agreement he observed gave him sufficient confidence to announce his result to the mathematical community.
 is clever and original. He essentially extended observations about finite polynomials and assumed that these same properties hold true for infinite series. Of course, Euler's original reasoning requires justification, but even without justification, by simply obtaining the correct value, he was able to verify it numerically against partial sums of the series. The agreement he observed gave him sufficient confidence to announce his result to the mathematical community.
is clever and original. He essentially extended observations about finite polynomials and assumed that these same properties hold true for infinite series. Of course, Euler's original reasoning requires justification, but even without justification, by simply obtaining the correct value, he was able to verify it numerically against partial sums of the series. The agreement he observed gave him sufficient confidence to announce his result to the mathematical community.
To follow Euler's argument, recall the Taylor series expansion of the sine function
Dividing through by x, we have
Now, the roots (zeros) of sin(x)/x occur precisely at  where
where  Let us assume we can express this infinite series as a (normalized) product of linear factors given by its roots, just as we do for finite polynomials:
Let us assume we can express this infinite series as a (normalized) product of linear factors given by its roots, just as we do for finite polynomials:
 where
where  Let us assume we can express this infinite series as a (normalized) product of linear factors given by its roots, just as we do for finite polynomials:
Let us assume we can express this infinite series as a (normalized) product of linear factors given by its roots, just as we do for finite polynomials:
If we formally multiply out this product and collect all the x2 terms (we are allowed to do so because of Newton's identities), we see that the x2 coefficient of sin(x)/x is
But from the original infinite series expansion of sin(x)/x, the coefficient of x2 is −1/(3!) = −1/6. These two coefficients must be equal; thus,
Multiplying through both sides of this equation by − π2 gives the sum of the reciprocals of the positive square integers.



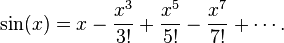

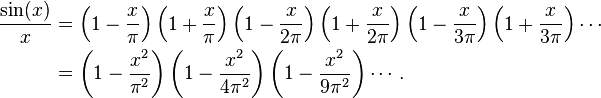
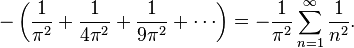


No comments:
Post a Comment