Theorem: The square root of 2 is irrational, 
Proof

Proof
Assume for the sake of contradiction that  . Hence
. Hence 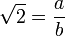 holds for some a and b that are coprime.
holds for some a and b that are coprime.
 . Hence
. Hence 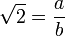 holds for some a and b that are coprime.
holds for some a and b that are coprime.
This implies that  . Rewriting this gives
. Rewriting this gives  .
.
 . Rewriting this gives
. Rewriting this gives  .
.
Since the left-hand side of the equation is divisible by 2, then so must the right-hand side, i.e.,  . Since 2 is prime, we must have that
. Since 2 is prime, we must have that  .
.
 . Since 2 is prime, we must have that
. Since 2 is prime, we must have that  .
.
So we may substitute a with  , and we have that
, and we have that 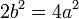 .
.
 , and we have that
, and we have that 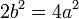 .
.
Dividing both sides with 2 yields  , and using similar arguments as above, we conclude that
, and using similar arguments as above, we conclude that  . However, we assumed that
. However, we assumed that 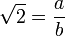 such that that a and b were coprime, and have now found that
such that that a and b were coprime, and have now found that  and
and  ; a contradiction.
; a contradiction.
 , and using similar arguments as above, we conclude that
, and using similar arguments as above, we conclude that  . However, we assumed that
. However, we assumed that 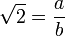 such that that a and b were coprime, and have now found that
such that that a and b were coprime, and have now found that  and
and  ; a contradiction.
; a contradiction.
Therefore, the assumption was false, and  cannot be written as a rational number. Hence, it is irrational.
cannot be written as a rational number. Hence, it is irrational.
 cannot be written as a rational number. Hence, it is irrational.
cannot be written as a rational number. Hence, it is irrational.
Another Proof
The following reductio ad absurdum argument is less well-known. It uses the additional information √2 > 1.
- Assume that √2 is a rational number. This would mean that there exist integers m and n with n ≠ 0 such that m/n = √2.
- Then √2 can also be written as an irreducible fraction m/n with positive integers, because √2 > 0.
- Then
 , because
, because  .
. - Since √2 > 1, it follows that m > n, which in turn implies that m > 2n – m.
- So the fraction m/n for √2, which according to (2) is already in lowest terms, is represented by (3) in strictly lower terms. This is a contradiction, so the assumption that √2 is rational must be false.
Similarly, assume an isosceles right triangle whose leg and hypotenuse have respective integer lengths n and m. By the Pythagorean theorem, the ratio m/n equals √2. It is possible to construct by a classic compass and straightedge construction a smaller isosceles right triangle whose leg and hypotenuse have respective lengths m − n and 2n − m. That construction proves the irrationality of √2 by the kind of method that was employed by ancient Greek geometers.

No comments:
Post a Comment