In mathematics, Descartes' rule of signs, first described by René Descartes in his work La Géométrie, is a technique for determining the number of positive or negative real roots of a polynomial.
The rule gives us an upper bound number of positive or negative roots of a polynomial. It is not a complete criterion, i.e. it does not tell the exact number of positive or negative roots.
Positive roots
The rule states that if the terms of a single-variable polynomial with real coefficients are ordered by descending variable exponent, then the number of positive roots of the polynomial is either equal to the number of sign differences between consecutive nonzero coefficients, or is less than it by a multiple of 2. Multiple roots of the same value are counted separately.
Negative roots
As a corollary of the rule, the number of negative roots is the number of sign changes after multiplying the coefficients of odd-power terms by −1, or fewer than it by a multiple of 2. This procedure is equivalent to substituting the negation of the variable for the variable itself: For example, to find the number of negative roots of 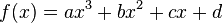 , we equivalently ask how many positive roots there are for
, we equivalently ask how many positive roots there are for  in
in 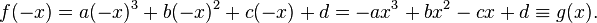 Using Descartes' rule of signs on
Using Descartes' rule of signs on  gives the number of positive roots
gives the number of positive roots 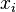 of g, and since
of g, and since 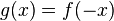 it gives the number of positive roots
it gives the number of positive roots  of f, which is the same as the number of negative roots
of f, which is the same as the number of negative roots 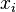 of f.
of f.
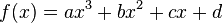 , we equivalently ask how many positive roots there are for
, we equivalently ask how many positive roots there are for  in
in 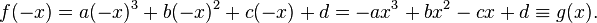 Using Descartes' rule of signs on
Using Descartes' rule of signs on  gives the number of positive roots
gives the number of positive roots 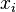 of g, and since
of g, and since 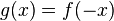 it gives the number of positive roots
it gives the number of positive roots  of f, which is the same as the number of negative roots
of f, which is the same as the number of negative roots 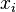 of f.
of f.Example
The polynomial
has one sign change between the second and third terms (the sequence of pairs of successive signs is ++, +−, −−). Therefore it has exactly one positive root. Note that the leading sign needs to be considered although in this particular example it does not affect the answer. To find the number of negative roots, change the signs of the coefficients of the terms with odd exponents, to obtain a second polynomial
This polynomial has two sign changes (the sequence of pairs of successive signs is −+, ++, +−), meaning that this second polynomial has two or zero positive roots; thus the original polynomial has two or zero negative roots.
In fact, the factorization of the first polynomial is
so the roots are −1 (twice) and 1.
The factorization of the second polynomial is
So here, the roots are 1 (twice) and −1, the negation of the roots of the original polynomial.
Complex roots
Since any nth degree polynomial has exactly n roots, the minimum number of complex roots is equal to
where p denotes the maximum number of positive roots, q denotes the maximum number of negative roots (both of which can be found using Descartes' rule of signs), and ndenotes the degree of the equation. A simple example is the polynomial
If 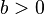 , this has no sign changes, and the polynomial does not change when odd-powered terms (of which there are none in this example) have their coefficients replaced by -x. Thus the maximum number of positive roots is zero, as is the maximum number of negative roots; so the minimum (and in this case exact) number of complex roots is
, this has no sign changes, and the polynomial does not change when odd-powered terms (of which there are none in this example) have their coefficients replaced by -x. Thus the maximum number of positive roots is zero, as is the maximum number of negative roots; so the minimum (and in this case exact) number of complex roots is  .
.
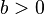 , this has no sign changes, and the polynomial does not change when odd-powered terms (of which there are none in this example) have their coefficients replaced by -x. Thus the maximum number of positive roots is zero, as is the maximum number of negative roots; so the minimum (and in this case exact) number of complex roots is
, this has no sign changes, and the polynomial does not change when odd-powered terms (of which there are none in this example) have their coefficients replaced by -x. Thus the maximum number of positive roots is zero, as is the maximum number of negative roots; so the minimum (and in this case exact) number of complex roots is  .
.







No comments:
Post a Comment