Cauchy Sequences

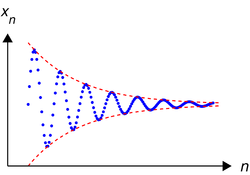
In mathematics, a Cauchy sequence , named after Augustin-Louis Cauchy, is a sequence whose elements become arbitrarily close to each otheras the sequence progresses. More precisely, given any small positive distance, all but a finite number of elements of the sequence are less than that given distance from each other.

The utility of Cauchy sequences lies in the fact that in a complete metric space (one where all such sequences are known to converge to a limit), the criterion for convergence depends only on the terms of the sequence itself. This is often exploited in algorithms, both theoretical and applied, where an iterative process can be shown relatively easily to produce a Cauchy sequence, consisting of the iterates.

The notions above are not as unfamiliar as they might at first appear. The customary acceptance of the fact that any real number x has a decimal expansion is an implicit acknowledgment that a particular Cauchy sequence of rational numbers (whose terms are the successive truncations of the decimal expansion of x) has the real limit x. In some cases it may be difficult to describe x independently of such a limiting process involving rational numbers.

Generalizations of Cauchy sequences in more abstract uniform spaces exist in the form of Cauchy filter and Cauchy net.

Real Numbers

A sequence

of real numbers is called Cauchy, if for every positive real number ε, there is a positive integer N such that for all natural numbers m, n >N

Metric Spaces

To define Cauchy sequences in any metric space X, the absolute value  is replaced by the distance  (whered : X × X → R with some specific properties, see Metric (mathematics)) between  and .

Formally, given a metric space (X, d), a sequence

is Cauchy, if for every positive real number ε > 0 there is a positive integer N such that for all natural numbers 

m,n > N, the distance

Roughly speaking, the terms of the sequence are getting closer and closer together in a way that suggests that the sequence ought to have a limit in X. Nonetheless, such a limit does not always exist within X.