Consider a matrix
This matrix has eigenvalues
So A is a 3-by-3 matrix with 3 different eigenvalues, therefore it is diagonalizable. Note that if there are exactly n distinct eigenvalues in an n×n matrix then this matrix is diagonalizable.
These eigenvalues are the values that will appear in the diagonalized form of matrix 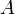 , so by finding the eigenvalues of
, so by finding the eigenvalues of 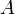 we have diagonalized it. We could stop here, but it is a good check to use the eigenvectors to diagonalize
we have diagonalized it. We could stop here, but it is a good check to use the eigenvectors to diagonalize 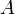 .
.
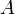 , so by finding the eigenvalues of
, so by finding the eigenvalues of 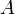 we have diagonalized it. We could stop here, but it is a good check to use the eigenvectors to diagonalize
we have diagonalized it. We could stop here, but it is a good check to use the eigenvectors to diagonalize 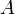 .
.
The eigenvectors of A are
One can easily check that 

Now, let P be the matrix with these eigenvectors as its columns:
Note there is no preferred order of the eigenvectors in P; changing the order of the eigenvectors in P just changes the order of the eigenvalues in the diagonalized form of A.
Then P diagonalizes A, as a simple computation confirms:
Note that the eigenvalues  appear in the diagonal matrix.
appear in the diagonal matrix.
 appear in the diagonal matrix.
appear in the diagonal matrix.Alternative Method
Starting with:  , where
, where ![P = [\vec{p_1}, \vec{p_2}]](http://upload.wikimedia.org/wikipedia/en/math/c/3/f/c3faca867a07dfa9e5587cfe69b3da60.png) , and the Diagonalization matrix
, and the Diagonalization matrix 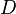 is:
is:
 , where
, where ![P = [\vec{p_1}, \vec{p_2}]](http://upload.wikimedia.org/wikipedia/en/math/c/3/f/c3faca867a07dfa9e5587cfe69b3da60.png) , and the Diagonalization matrix
, and the Diagonalization matrix 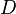 is:
is:
Distribute 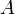 into the column vectors of
into the column vectors of 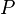 .
.
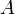 into the column vectors of
into the column vectors of 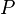 .
.
Then 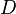 can be broken down to its column vectors as follows:
can be broken down to its column vectors as follows:
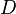 can be broken down to its column vectors as follows:
can be broken down to its column vectors as follows:
Multiplying 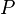 on the left side of the equation gives:
on the left side of the equation gives:
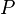 on the left side of the equation gives:
on the left side of the equation gives:
Setting each entry of the matrix to its corresponding entry:
Then the equations can be solved as follows, using the same process for both:
and it solves for  , which is the first entry in the diagonal matrix, and also the first eigenvalue.
, which is the first entry in the diagonal matrix, and also the first eigenvalue.
 , which is the first entry in the diagonal matrix, and also the first eigenvalue.
, which is the first entry in the diagonal matrix, and also the first eigenvalue.






![PD = [A\vec{p_1},A\vec{p_2}]](http://upload.wikimedia.org/wikipedia/en/math/a/f/3/af37d3ac0db710a2722222b9860783f4.png)
![P[d_{11}\vec{e_1},d_{22}\vec{e_2}] = [A\vec{p_1},A\vec{p_2}]](http://upload.wikimedia.org/wikipedia/en/math/3/4/5/34596439874fe5d08a7e9ca0aba963a6.png)
![[\vec{d_{11}}\vec{p_1}, \vec{d_{22}}\vec{p_2}] = [A\vec{p_1},A\vec{p_2}]](http://upload.wikimedia.org/wikipedia/en/math/c/3/6/c368a7873fd72b1a7957f34d3d609f29.png)




No comments:
Post a Comment