In geometry, a Steiner chain is a set of n circles, all of which are tangent to two given non-intersecting circles (blue and red in Figure 1), where n is finite and each circle in the chain is tangent to the previous and next circles in the chain. In the usualclosed Steiner chains, the first and last (nth) circles are also tangent to each other; by contrast, in open Steiner chains, they need not be. The given circles α and β do not intersect, but otherwise are unconstrained; the smaller circle may lie completely inside or outside of the larger circle. In these cases, the centers of Steiner-chain circles lie on an ellipse or a hyperbola, respectively.
Steiner chains are named after Jakob Steiner, who defined them in the 19th century and discovered many of their properties. A fundamental result is Steiner's porism, which states:
-
- If at least one closed Steiner chain of n circles exists for two given circles α and β, then there is an infinite number of closed Steiner chains of n circles; and any circle tangent to α and β in the same way is a member of such a chain.
"Tangent in the same way" means that the arbitrary circle is internally or externally tangent in the same way as a circle of the original Steiner chain. A porism is a type of theorem relating to the number of solutions and the conditions on it. Porisms often describe a geometrical figure that cannot exist unless a condition is met, but otherwise may exist in infinite number; another example is Poncelet's porism.
The method of circle inversion is helpful in treating Steiner chains. Since it preserves tangencies, angles and circles, inversion transforms one Steiner chain into another of the same number of circles. One particular choice of inversion transforms the given circles α and β into concentric circles; in this case, all the circles of the Steiner chain have the same size and can "roll" around in the annulus between the circles similar to ball bearings. This standard configuration allows several properties of Steiner chains to be derived, e.g., its points of tangencies always lie on a circle. Several generalizations of Steiner chains exist, most notably Soddy's hexlet and Pappus chains.
Elliptical and Hyperbolic Locus of Centers
The centers of the circles of a Steiner chain lie on a conic section. For example, if the smaller given circle lies within the larger, the centers lie on an ellipse. This is true for any set of circles that are internally tangent to one given circle and externally tangent to the other; such systems of circles appear in the Pappus chain, the problem of Apollonius, and the three-dimensional Soddy's hexlet. Similarly, if some circles of the Steiner chain are externally tangent to both given circles, their centers must lie on a hyperbola, whereas those that are internally tangent to both lie on a different hyperbola.
The circles of the Steiner chain are tangent to two fixed circles, denoted here as α and β, where β is enclosed by α. Let the radii of these two circles be denoted as rα and rβ, respectively, and let their respective centers be the points A and B. Let the radius, diameter and center point of the kth circle of the Steiner chain be denoted as rk, dk and Pk, respectively.
All the centers of the circles in the Steiner chain are located on a common ellipse, for the following reason.The sum of the distances from the kth circle of the Pappus chain to the two centers A and B of thefixed circles equals a constant
Thus, for all the centers of the circles of the Steiner chain, the sum of distances to A and B equals the same constant, rα+rβ. This defines an ellipse, whose two foci are the points A and B, the centers of the circles, α and β, that sandwich the Steiner chain of circles. The property of having centers on an ellipse is common to all situations where a series of circles is tangent to two fixed circles, such as the related Pappus chain of circles and the three-dimensional Soddy's hexlet.
The sum of distances to the foci equals twice the semi-major axis a of an ellipse; hence,
- 2a = rα + rβ
Let p equal the distance between the foci, A and B. Then, the eccentricity e is defined by 2 ae = p, or
From these parameters, the semi-minor axis b and the semi-latus rectum L can be determined
Therefore, the ellipse can be described by an equation in terms of its distance d to one focus
where θ is the angle with the line joining the two foci.






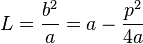

No comments:
Post a Comment