The divine proportion appears in Fibonacci's 1202 book on financial mathematics, the Liber Abaci. The Liber is a series of increasingly difficult problems (with solutions) that generations of apprentice merchants used to learn their trade in the middle ages. It was the textbook that taught Copernicus, who wrote about money before he wrote about planets, and Simon Stevin(1548 – 1620), who made mathematics useful and helped free the Netherlands from Spain.
One of the simpler problems Fibonacci used was on the business of breeding rabbits. Given that one pair of rabbits produces one other pair of rabbits a month, how many rabbits will there be after a year, assuming that we start with one pair?
The model Fibonacci is using is that a pair of rabbits take a month to become mature. They then mate and the rabbit pregnancy lasts a month. So:
At the start (month zero): There is one pair of immature rabbits.
First month: The pair mature and mate.
Second month: A new pair is born to the original pair, so there are two pairs.
Third month: The original pair parent a new pair, the second pair reach maturity. In total there are three pairs.
Fourth month: The original and second pair have offspring, the third pair reach maturity. In all there are five pairs.
Carrying on this rule, Fibonacci calculated the number of rabbits at the start of each month as
Carrying on this rule, Fibonacci calculated the number of rabbits at the start of each month as
| Month | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Pairs | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | 55 | 89 | 144 | 233 |
This is the famous Fibonacci sequence. Each number in the sequence is calculated by adding together the preceding two numbers, for example the numbers after 233 would be 144 + 233 = 377 and then 233 + 377 = 610. What medieval merchants realised is that as you move along the sequence, the ratio of successive numbers approaches a number which had already been known to the ancient Greeks: the golden ratio.
The golden ratio first appears in proposition 30 of book VI of Euclid's Elements. Written around 300BC the Elements is the oldest maths text book and it is also the most influential one ever produced.
In book VI Euclid solves the problem of dividing a line up such that the ratio of the longer segment to the whole line is equal to the ratio of the smaller segment to the longer segment. For example, if we have a line of length 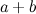 where the length
where the length  is bigger than the length
is bigger than the length 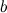 , we want.
, we want.
We use the symbol 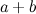 where the length
where the length  is bigger than the length
is bigger than the length 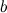 , we want.
, we want.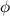 to define this golden ratio.
to define this golden ratio.
It is quite easy to see that the golden ration is the limit of successive ratios in Fibonacci's sequence
But Euclid’s golden ratio is also Brown’s divine proportion. To see this, remember we have defined 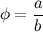 and so
and so 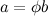 . Now substitute this into the original expression
. Now substitute this into the original expression
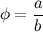 and so
and so 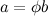 . Now substitute this into the original expression
. Now substitute this into the original expression![\[ \frac{\phi b+b}{\phi b}=\frac{\phi b}{b}. \]](http://plus.maths.org/MI/03596b6401a74f9410c27e0db796133a/images/img-0003.png) |
Cancelling the 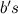 gives
gives
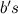 gives
gives![\[ \frac{\phi + 1}{\phi }=\phi \]](http://plus.maths.org/MI/03596b6401a74f9410c27e0db796133a/images/img-0005.png) |
or
![\[ \phi ^2-\phi -1=0. \]](http://plus.maths.org/MI/03596b6401a74f9410c27e0db796133a/images/img-0006.png) |
The positive solution to this equation is
![\[ \phi =\frac{1+\sqrt {5}}{2}\approx 1.610339887... . \]](http://plus.maths.org/MI/03596b6401a74f9410c27e0db796133a/images/img-0007.png) |
Euclid would not have, could not have done this calculation, not least because the Greeks did not use decimals. Euclid would have tackled the problem in a different way. The equation
![\[ \phi ^2-\phi -1=0 \]](http://plus.maths.org/MI/94f31f7482ee1318d46878091e2c440f/images/img-0001.png) |
can be re-arranged to give
![\[ \phi =1+\frac{1}{\phi }. \]](http://plus.maths.org/MI/94f31f7482ee1318d46878091e2c440f/images/img-0002.png) |
Now, the denominator on the right is the same as the left hand side of the equality, so
![\[ \phi =1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{\phi }} \]](http://plus.maths.org/MI/94f31f7482ee1318d46878091e2c440f/images/img-0003.png) |
and again, and again, ...
![\[ \phi =1+\frac{1}{1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{1+\displaystyle \frac{1}{\phi }}}}. \]](http://plus.maths.org/MI/94f31f7482ee1318d46878091e2c440f/images/img-0004.png) |
Continuing in this way gives you an infinite expression involving only 1’s.
A number written in this way is called a continued fraction. The Greeks sometimes used continued fractions to write down non-integers. Euclid would have realised that 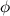 was irrational (or incommensurable as he would have put it) because it never ended. What is more, it is a continued fraction made up only of 1’s.
was irrational (or incommensurable as he would have put it) because it never ended. What is more, it is a continued fraction made up only of 1’s.
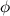 was irrational (or incommensurable as he would have put it) because it never ended. What is more, it is a continued fraction made up only of 1’s.
was irrational (or incommensurable as he would have put it) because it never ended. What is more, it is a continued fraction made up only of 1’s.
This is why the Da Vinci Code is so ridiculous. If Robert Langdon, the book’s hero, was such an expert on symbols he would never present 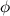 as a meaningless decimal, but as a continued fraction made up only of 1s. Why? Because 1 was highly symbolic to Christians as it represented the "one God". This is why the golden ratio is divine, because it is god’s number, not because there is a natural or super-natural significance of the ratio
as a meaningless decimal, but as a continued fraction made up only of 1s. Why? Because 1 was highly symbolic to Christians as it represented the "one God". This is why the golden ratio is divine, because it is god’s number, not because there is a natural or super-natural significance of the ratio
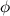 as a meaningless decimal, but as a continued fraction made up only of 1s. Why? Because 1 was highly symbolic to Christians as it represented the "one God". This is why the golden ratio is divine, because it is god’s number, not because there is a natural or super-natural significance of the ratio
as a meaningless decimal, but as a continued fraction made up only of 1s. Why? Because 1 was highly symbolic to Christians as it represented the "one God". This is why the golden ratio is divine, because it is god’s number, not because there is a natural or super-natural significance of the ratio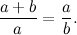

No comments:
Post a Comment