yourMATHsolver: Cayley–Hamilton theorem

In linear algebra, the Cayley–Hamilton theorem (named after the mathematicians Arthur Cayley and William Hamilton) states that every square matrix over a commutative ring (such as the real or complex field) satisfies its own characteristic equation.

More precisely:

If A is a given n×n matrix and I_n is the n×n identity matrix, then the characteristic polynomial of A is defined as

$p(\lambda)=\det(\lambda I_n-A)\,$

where "det" is the determinant operation. Since the entries of the matrix are (linear or constant) polynomials in λ, the determinant is also a polynomial in λ. The Cayley–Hamilton theorem states that "substituting" the matrix A for λ in this polynomial results in the zero matrix:

$p(A)=0.\,$

The powers of λ that have become powers of A by the substitution should be computed by repeated matrix multiplication, and the constant term should be multiplied by the identity matrix (the zeroth power of A) so that it can be added to the other terms. The theorem allows Aⁿ to be expressed as a linear combination of the lower matrix powers of A.

When the ring is a field, the Cayley–Hamilton theorem is equivalent to the statement that the minimal polynomial of a square matrix divides its characteristic polynomial.

Example

As a concrete example, let

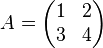$A = \begin{pmatrix}1&2\\3&4\end{pmatrix}$ .

Its characteristic polynomial is given by

$p(\lambda)=\det(\lambda I_2-A)=\det\begin{pmatrix}\lambda-1&-2\\ -3&\lambda-4\end{pmatrix}=(\lambda-1)(\lambda-4)-(-2)(-3)=\lambda^2-5\lambda-2.$

The Cayley–Hamilton theorem claims that, if we define

p (X) = X 2 - 5 X - 2 I 2,

then

$p(A)=A^2-5A-2I_2=\begin{pmatrix}0&0\\0&0\\\end{pmatrix},$

which one can verify easily.

A direct algebraic proof

This proof uses just the kind of objects needed to formulate the Cayley–Hamilton theorem: matrices with polynomials as entries. The matrix

t I n - A

whose determinant is the characteristic polynomial of A is such a matrix, and since polynomials form a commutative ring, it has an adjugate

$B=\mbox{adj}(tI_n-A).\,$

Then according to the right hand fundamental relation of the adjugate one has

$(t I_n - A) \cdot B = \det(t I_n - A) I_n = p(t) I_n.$

Since B is also a matrix with polynomials in t as entries, one can for each i collect the coefficients of

t i

in each entry to form a matrix B_i of numbers, such that one has

$B = \sum_{i = 0}^{n - 1} t^i B_i \,$

(the way the entries of B are defined makes clear that no powers higher than

t n - 1

occur). While this looks like a polynomial with matrices as coefficients, we shall not consider such a notion; it is just a way to write a matrix with polynomial entries as linear combination of constant matrices, and the coefficient

t i

has been written to the left of the matrix to stress this point of view. Now one can expand the matrix product in our equation by bilinearity

$\begin{align} p(t) I_n &= (t I_n - A) \cdot B \\ &=(t I_n - A) \cdot\sum_{i = 0}^{n - 1} t^i B_i \\ &=\sum_{i = 0}^{n - 1} tI_n\cdot t^i B_i - \sum_{i = 0}^{n - 1} A\cdot t^i B_i \\ &=\sum_{i = 0}^{n - 1} t^{i + 1} B_i- \sum_{i = 0}^{n - 1} t^i A\cdot B_i \\ &=t^n B_{n - 1} + \sum_{i = 1}^{n - 1} t^i(B_{i - 1} - A\cdot B_i) - A \cdot B_0. \end{align}$

Writing $p(t)I_n=t^nI_n+t^{n-1}c_{n-1}I_n+\cdots+tc_1I_n+c_0I_n$ , one obtains an equality of two matrices with polynomial entries, written as linear combinations of constant matrices with powers of t as coefficients. Such an equality can hold only if in any matrix position the entry that is multiplied by a given power

t i

is the same on both sides; it follows that the constant matrices with coefficient

t i

in both expressions must be equal. Writing these equations for i from n down to 0 one finds

$B_{n - 1} = I_n, \qquad B_{i - 1} - A\cdot B_i = c_i I_n\quad \mbox{for }0 < i < n, \qquad -A B_0 = c_0 I_n. \,$

We multiply the equation of the coefficients of tⁱ from the left by Aⁱ, and sum up; the left-hand sides form a telescoping sum and cancel completely, which results in the equation

$0=A^n+c_{n-1}A^{n-1}+\cdots+c_1A+c_0I_n= p(A).$

This completes the proof.

Pages

Wednesday, December 21, 2011

Cayley–Hamilton theorem

A direct algebraic proof

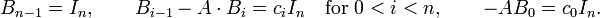
No comments:

Post a Comment